Understanding limits of functions is a fundamental concept in calculus that is crucial for mastering more advanced topics in mathematics. To effectively study and grasp the intricacies of limits, it is essential to utilize proven study methods that promote comprehension and retention of key concepts.
In this article, we will explore three highly effective study methods that have been shown to enhance understanding of limits of functions. By incorporating these strategies into your study routine, you can improve your grasp of this important mathematical concept and set yourself up for success in your calculus studies.
1. Overview of Limits of Functions
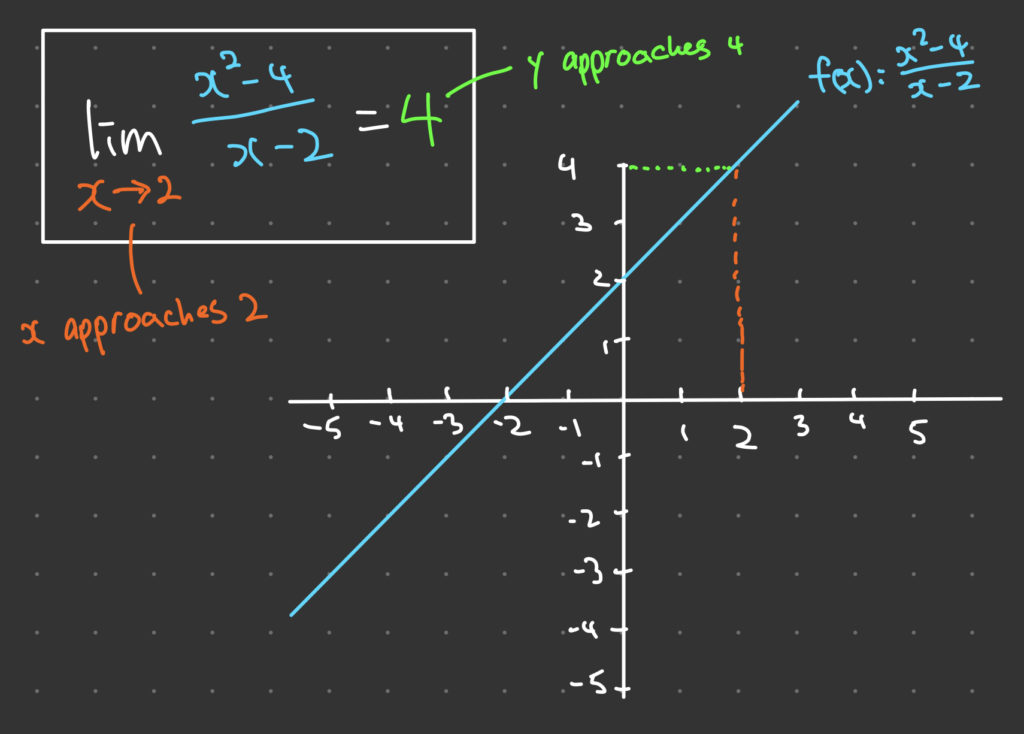
Understanding limits of functions is crucial in calculus as it allows us to determine the behavior of a function as it approaches a certain value.
Limits of functions help us analyze and predict the values of functions at specific points, and play a significant role in calculus concepts such as continuity and differentiation. In this article, we will explore three effective study methods that can aid in mastering the concept of limits of functions.
Whether you are a student struggling with calculus or a math enthusiast looking to deepen your understanding, these methods will provide you with practical strategies to approach and solve problems related to limits of functions.
2. Visual Representation of Limits through Graphs
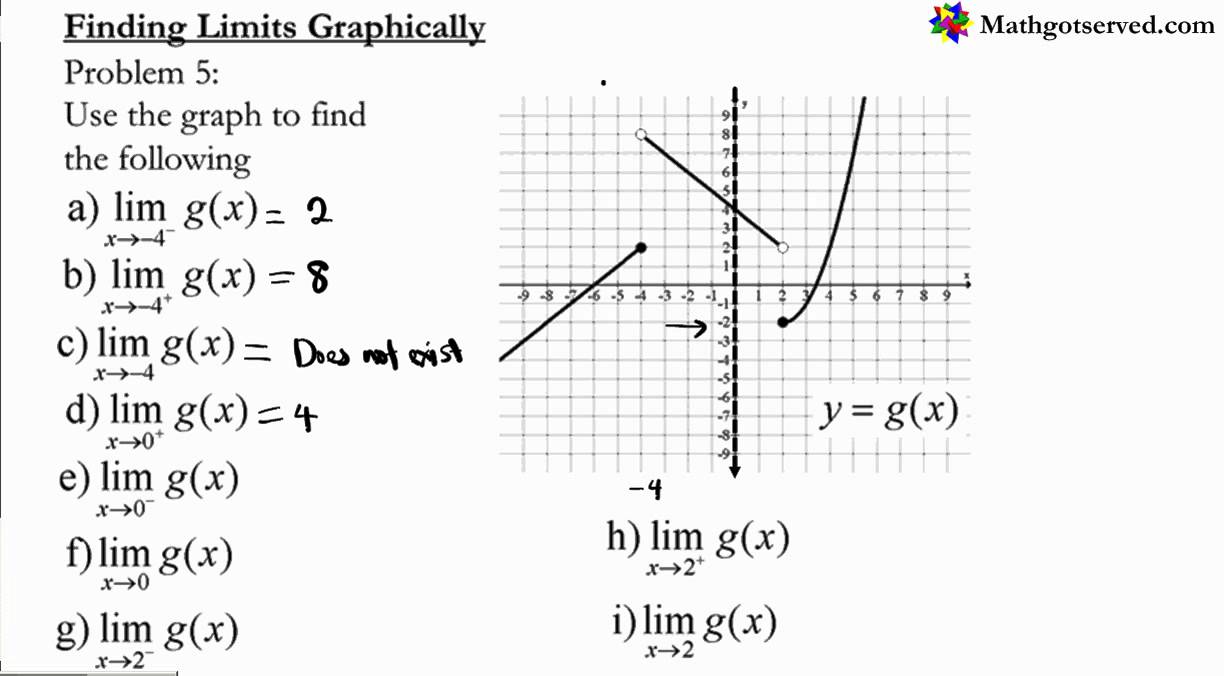
Visual representation of limits through graphs plays a crucial role in understanding the behavior of functions.
Graphs provide a clear and intuitive way to see how a function approaches a particular value as its input approaches a specific point. By examining the trend of the graph near the limit point, students can gain insights into the limits of functions and how they may behave in different scenarios.
This visual approach helps to cement the concepts of limits and provides a practical way to visualize abstract mathematical ideas. By looking at the graph, students can grasp the concept of limits more effectively and develop a deeper understanding of the topic.
3. Techniques for Solving Limit Problems
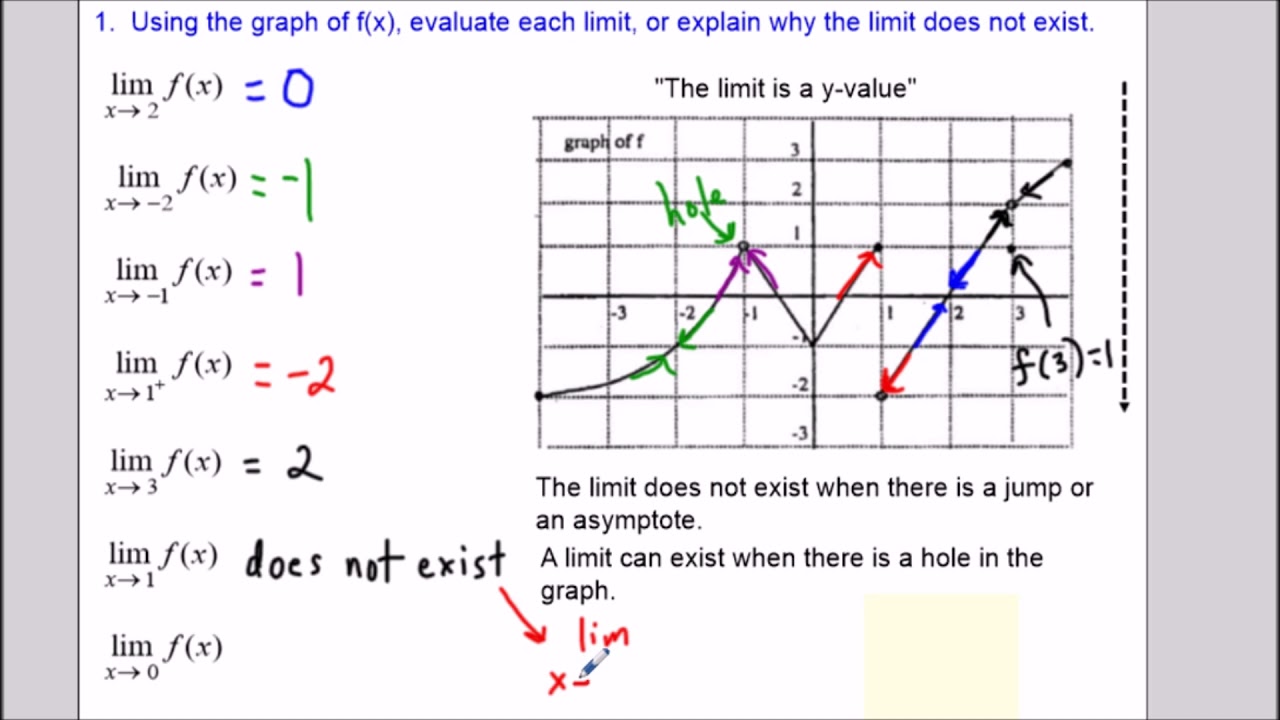
When approaching limit problems, it is essential to have a variety of techniques at your disposal in order to effectively solve them.
One common method is the use of algebraic manipulation to simplify complex expressions and identify patterns that can help determine the limit. Another helpful technique is using trigonometric identities or properties to simplify trigonometric functions and make calculating limits more manageable.
Additionally, employing LHôpitals Rule can be useful when faced with indeterminate forms that involve ratios of functions. By familiarizing yourself with these techniques and practicing with a variety of limit problems, you can improve your problem-solving skills and gain a better understanding of limit’s of functions.
Conclusion
In conclusion, mastering the understanding of limits of functions is essential in calculus and requires consistent practice and study. The three effective study methods discussed in this article, namely breaking down the concept into smaller parts, utilizing visualization techniques, and practicing with diverse exercises on notable limits, can greatly improve one’s comprehension and proficiency in this fundamental topic. By incorporating these methods into their study routine, students can enhance their problem-solving skills, deepen their understanding of calculus concepts, and ultimately succeed in their academic endeavors.
With dedication and perseverance, anyone can gain a solid grasp of limits and excel in calculus.


